 Figure 1.1
Figure 1.1 In these lectures we'll learn algebraic methods for representing and computing with geometric objects. Of course we're interested in geometry mainly because the rotations and translations of the eyes and head are motions in real physical space, but the geometric algebra we'll learn will also apply to many subjects that are not literally spatial; in fact any situation that can be plotted in a graph can be regarded as existing in an abstract space, and can be handled geometrically. This spatial metaphor has been powerful in many domains: we think of time, or of musical tones, as a line; we think of colour as a wheel; we measure correlations between variables by plotting them and examining the resulting curve. And the metaphor seldom goes the other way: we rarely try to explain spatial concepts, like the way to the cafeteria, by humming a tune or waving coloured streamers. Apparently "space" is an unusually potent concept, perhaps because our minds are well suited to picturing complex relations in spatial form.
Geometric algebra starts from one fundamental class of object. When our Stone Age forebears gathered for their versions of these talks they considered various possibilities for Fundamental Geometric Object, including
With the benefit of ten thousand years of mathematical experience, we'll make a choice which would not have been obvious to primitive hunter-gatherers: we'll bundle together the notions of magnitude and direction into a single object: a directed magnitude, or vector.
Vectors can be used to represent many sorts of spatial objects with magnitude and direction, such as forces, velocities and translations. Physical things like these were the original inspiration for the vector concept, but the modern mathematical definition of a vector was obtained by a long process of abstraction - ie of distilling the essence that is common to these various physical objects - with the result that the modern concept of a vector is very general, applying to all sorts of things that you would never think of as "directed magnitudes". Unfortunately, the modern definition of a vector is also very abstruse, and seems at first glance to have nothing to do with space at all. In the next section we'll look briefly at the modern abstract definition of a vector, but for now we'll continue to work with the intuitive idea of a directed magnitude, from which the modern abstractions were derived.
Vector algebra begins when we define operations on our vectors. The two most basic operations, which we'll consider in this chapter, are addition and scalar multiplication.
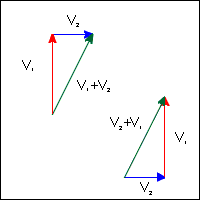
Addition of two vectors, v1 and v2 (we follow the usual convention of representing vectors with boldface letters), is shown in Figure 1.1.
 Figure 1.1
Figure 1.1
We take two arrows representing v1 and v2 and place them head to tail as shown on the left of the figure. Then the arrow from the tail of v1 to the head of v2 represents the sum v1 + v2. The right side of Fig. 1.1 makes the point that adding the same two vectors in the opposite order yields the same sum ie v1 + v2 = v2 + v1; we say therefore that addition of vectors is commutative. This method of adding vectors by drawing arrows has a pleasing intuitive feel, but it is inconvenient because you need lots of paper and a ruler, and it is difficult to be precise even with a very sharp pencil. In Section 1.5 (Coordinate Systems) we'll learn how to express vectors in terms of numbers, known as coordinates, with the result that our vector operations will then be computable by arithmetic.
Vector addition has many physical applications. For example, if v1 and v2 represent two translations of an object in space, then v1 + v2 is the overall translation achieved by first carrying out v1 and then v2. Or if our vectors represent forces (or torques), it is an empirical fact that two simultaneously-applied forces (or torques) combine to act like the vector sum of the individual forces (or torques).
The second algebraic operation on vectors is scalar multiplication. Any vector v can be multiplied by any scalar (ie real number) s, to yield a new vector sv, s times as long as v, and pointing along the same line. If s > 0 then sv points in the same direction as v; if s < 0 then sv and v point in opposite directions; if s = 0 then sv = 0, the zero vector, which has no direction. Real numbers are called scalars in this context because they scale vectors; that is, they stretch or contract or reverse vectors without rotating them.
1.3 Vector Spaces
An odd feature of mathematics is that many objects cannot be defined alone, but are characterized by their relations to a large number of other objects in a set. For example, we don't define a vector directly; rather we define a set of things called a vector space. A vector is then defined as anything that is a member of the vector space. A vector space is any set of objects (called V below) that satisfies the following 10 axioms VS1-10. Try to figure out the intuitive geometric property of directed magnitudes that inspired each axiom.
VS1. If u and v are objects in V, then u + v is in V
VS2. u + v = v + u
VS3. u + (v + w) = (u + v) + w
VS4. There is an object 0 in V such that v + 0 = v for all v in V
VS5. For each v in V, there is an object -v in V, called the negative of v, such that v + -v = 0
VS6. If s is any scalar and v is any object in V, then sv is in V
VS7. s(u + v) = su + sv
VS8. (r + s)v = rv + sv
VS9. r(su) = (rs)u
VS10. 1v = v
Many of these properties have names. For example, VS1 says that V is closed under addition; VS2 says that addition is commutative (ie order does not matter); VS3 says addition is associative (ie placement of parentheses is irrelevant); and VS7 and VS8 are called distributive laws.
Example 1.1. The set of all n-tuples of real numbers, written Rn, is a vector space, if addition and scalar multiplication are defined in the obvious way. For example, it is easy to confirm that R3 is a vector space with addition and scalar multiplication defined by (v1, v2, v3) + (w1, w2, w3) = (v1 + w1, v2 + w2, v3 + w3) and s(v1, v2, v3) = (sv1, sv2, sv3).
Abstract vectors, defined by the above 10 axioms, sometimes clash with our intuitions about what is a vector. For example, by the above definition, the set of all polynomial functions (0, 1, x, x2, x + x2 etc.) is a vector space, even though polynomials bear little superficial resemblance to directed magnitudes. On the other hand rotations, which do have magnitude and direction like intuitive vectors, do not share the "deeper" properties encapsulated in axioms VS1-10 (which axioms fail?), and so are not vectors after all. What are they then? Before we can answer this question, we need to know a little more about vectors.
If we choose any three vectors e1, e2 and e3 that don't lie in a single plane (eg e1 = 1 m in the northward direction, e2 = 1 m west, e3 = 1 m up), then any vector in 3-dimensional (3D) space can be expressed as a sum of scalar multiples of the 3 e vectors. Essentially, this is what it means to say the space is 3-D. The set of e vectors, out of which all other vectors can be built, is called a basis for the space. Every vector space has infinitely many different bases (eg for 3-D space, we could also have e1 = 1 m northwest, e2 = 3 m south, e3 = any vector not in the horizontal plane). Some sample bases for a 2-D space are shown in Figure 1.2.
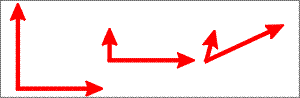 Figure 1.2
Figure 1.2
Note that the basis vectors need not have the same length and do not have to be orthogonal, although in practice we will always choose bases composed of orthogonal vectors of length 1 because they simplify our computations. Such bases are called orthonormal.
Using bases, we can define the notion of a coordinate system for a vector space. Thus suppose V is an n-dimensional vector space with basis B = < e1,..., en >. By the definition of a basis, any vector v in V can be written as a combination of scalar multiples of the vectors in B:
v = v1e1 + v2e2 + ... + vnen, (1.1)
where the nonboldface v's with subscripts are real numbers, called the coordinates or components of v with respect to the basis B. Obviously, if we chose a different basis B' for V, the coordinates of v with respect to B' would in general be different from its coordinates with respect to B. When we change the basis, we change the coordinate system. This issue will be addressed in more detail in a later lecture when we learn to express eye position and velocity vectors in magnetic field coordinates, in head coordinates and in Listing's coordinates.
Coordinates provide a convenient means for computing with vectors. For example, suppose V is a 3-D space, and a basis for V has been chosen. Then if v = (v1, v2, v3) and w = (w1, w2, w3) we have
v + w = (v1 + w1, v2 + w2, v3 + w3) (1.2)
because (using properties VS3, VS2 and VS8):
(v1e1 + v2e2 + v3e3) + (w1e1 + w2e2 + w3e3)
= (v1 + w1)e1 + (v2 + w2)e2 + (v3 + w3)e3. (1.3)
Similarly we can show that
sv = (sv1, sv2, sv3). (1.4)
Problem 1.1. If e1, e2 and e3 form a basis for a 3-D space, what are the coordinates of the three basis vectors themselves relative to this basis?
Problem 1.2. If we have the orthogonal vectors e1 = 1 unit forward, e2 = 1 unit left, e3 = 1 unit up, then e1, e2 and e3 form a basis -- called the standard basis for 3-D physical space. If v is the vector that is obtained by rotating e3 30° leftward in the horizontal plane, what are the coordinates of v relative to the standard basis?