5.1 Flipped Reflections

So far, you've been led through some of the linear algebra that every math student's dog learns in first year. In this chapter and the next, you'll be hurled through a region of the mathematical galaxy that is much less travelled, and that, in fact, is still imperfectly charted and rather controversial. The point of these chapters is not to make you a master of weird algebras, but to prepare you for your encounter with quaternions in Chapter 7. It would be possible to become adept with quaternions without this detour, but I want to minimize the feeling you would otherwise have that quaternions have sprung out of nothing, like Aphrodite, and that their ability to yield correct answers about rotations is pure magic. In these chapters I'll try to show you the connection between quaternions and everyday linear algebra, and I'll try to give you the illusion that, if you'd had enough time and nothing better to do, you could have discovered quaternions yourself.

The first thing that would set you on the trail to quaternions would be a funny feeling, like Sherlock Holmes used to have, that something fishy happened back in Chapter 2. Near the end of that chapter, you were introduced to the idea of a cross product, and you discovered that the cross product, unlike all the other vector operations we have met, is defined only in 3-D space. Also, unlike all the other products we have encountered, cross multiplication is not associative. These things struck you as peculiar, but you thought nothing more of them at the time. Later, in Equation (4.3), you learned that a reflection reverses cross products. Let us consider this in more detail.

Figure 5.1a shows a mirror with some vectors reflected in it. On the near side of the mirror are e₁, e₂ and their cross product, e₃. Through the looking glass are the reflections: e₁', e₂' and e₃'. But in the mirror world, of course, e₁' × e₂' is not e₃' but -e₃', as you can show using the right hand rule. Thus the cross product on one side of the mirror points up and on the other side it points down.

Does it seem strange to you that an upward-pointing vector can flip over when reflected in a vertical mirror? Of course, lots of crazy things happen in mathematics, but if you are bothered by this upside-down reflection, your intuition is sound: there is something odd here. The solution, as we'll later see, is that, despite what you learned in High School and in Chapter 2, the cross product e₁ × e₂ is, in a sense, not really e₃. Actually, it's not really a vector at all, but a new, vampire-like thing that's hard to distinguish from a vector except when it stands in front of a mirror. There are other examples of these strange beings living in our midst, the most important being angular velocity "vectors". Figures 5.1b-d show that angular velocities also flip over when they go through mirrors. What are these things with the flipped reflections? To answer this question we have to go back and look very carefully at the whole idea of a "product" of vectors.

5.2 Steps Toward a Vector Product: Area and Signed Area

What, intuitively, could it mean to multiply two vectors together to get their "product"? Clearly, one way to combine vectors is to add them. Is there any other sensible way to combine vectors and get something new? One possibility that seems promising is this: two vectors (as long as they're not parallel) determine a plane. Maybe the product of two vectors should be, somehow, a plane.

But surely the product of two vectors should have some sort of magnitude, and when we, say, double the size of one of the vectors, the product should also double in size, right? All the products we have so far considered, including dot and cross products, matrix products and ordinary products of numbers have this property: when you multiply one of the factors by a scalar s, the product is also multiplied by s. (This does not hold for number, vector or matrix sums, but only for operations that we call products). With this in mind, note that two vectors give us more than just a plane: if we draw the vectors head to tail they determine a parallelogram in the plane with a particular area (Figure 5.2), and if we double the length of one of the vectors, the area doubles.

We'll write A(v, w) to represent the area of the parallelogram determined by the two vectors v and w. To start with, it will be useful to restrict our attention to vectors in 2-D space. Thus we can regard A as a function acting on a pair of 2-component vectors to yield a real number. We are interested in the properties of this 2-D area function. Note first that, as shown in Figure 5.2:

A(v₁ + v₂, w) = A(v₁, w) + A(v₂, w) (5.1)

and

A(sv, w) = sA(v, w) for s > 0 (5.2)

Equation (5.2) generalizes the fact that doubling the length of an input vector doubles the area. We require that s be greater than 0 in Equation (5.2), because, at least at first glance, the idea of negative area doesn't make much sense, but we'll return to this point shortly. Now except for the restriction that s > 0, the above equations show that A is a linear function of its first input if the second input, w, is held constant. Similarly, one can show that A is also a linear function of the second input when the first is held constant. A 2-input function that is linear in each input when the other is held constant is called bilinear, and when we encounter such a function, we usually call it a "product". Thus the dot, cross, matrix and ordinary number products are bilinear functions.

Our 2-D area function A is almost a bilinear function, the only problem being that s was not allowed to be negative in Equation (5.2), because our intuitions could not handle the idea of negative area. But bilinearity is such a convenient property that it pays to stretch our intuitions to accomodate it. Therefore, we'll replace the intuitive idea of area with the more useful notion of signed area, which behaves like area except that it obeys (5.1) and (5.2). Thus A is not the area function but the signed area function in 2-D space. We'll see that the extra information (the sign) has geometric significance, specifying what is called the "orientation" of the parallelogram formed by v and w.

An important property of the signed area function A is

A(v, v) = 0 (5.3)

That is, if we put the same vector in both input slots of the function A, we get zero, because the "parallelogram" formed by v and itself is flat, with area zero. As a direct consequence of (5.3) we have

A(v, w) = -A(w, v) (5.4)

That is, switching the order of the two inputs reverses the sign of the output. The proof runs as follows: 0 = A(v + w, v + w) (by (5.3)) = A(v, v) + A(v, w) + A(w, v) + A(w, w) (by 5.1) = A(v, w) + A(w, v) (by (5.3)). Thus A is anticommutative.

5.3 Achieving a Vector Product: Bivectors

We've seen that our 2-D signed area function A is bilinear, but what about the 3-D signed area function, which takes to vectors in 3-D space and yields the signed area of their parallelogram? Observe that the parallelogram formed by e₁ and e₂, and that formed by e₁ and e₃, both have area 1. Thus A(e₁, e₂) and A(e₁, e₃) are both equal to 1 (or maybe -1; we haven't yet learned how to determine the sign of a signed area), and so their sum is 2 (or maybe 0 or -2), but A(e₁, e₂ + e₃) = + . Thus Equation (5.1) fails, and so the 3-D signed area function is not bilinear.

After this disappointment, you may feel that bilinearity obviously has nothing to do with area, and the attempt to force it by introducing "signed" area was artificial and misguided. But in fact bilinearity is deeply connected with the concept of area, and we can see this if we persevere in our attempt to get a bilinear area function that works in all dimensions. The problem is that, as we observed at the start, two vectors don't just determine a parallelogram with a particular (signed) area, they determine a parallelogram in a particular plane. The reason bilinearity fails for the 3-D signed area function is that this function carries no information about the plane of the input vectors.

The next step, therefore, is to replace signed area with the even richer concept of a bivector, which contains all the information of the signed area plus information about the plane containing the two input vectors. Bivectors can be explained by analogy with vectors as follows: we specify a vector by choosing a line (e.g. the interaural line), a "sign" or direction along that line (e.g. left as opposed to right), and a magnitude or length along the line. Similarly, we can specify a bivector by choosing a plane and a signed area in that plane. Thus while a vector is a "fusion" of a line with a "signed length", i.e. a length and a direction, a bivector is the fusion of a plane with a signed area. The best way to make this notion precise is to give the rules for manipulating bivectors.

We write v ^ w, called the exterior or wedge product of the vectors v and w, for the bivector determined by v and w, in that order. This important vector operation, which was discovered in the middle of the last century by a German schoolteacher and human cannonball named Skeezix Grassmann and was later long ignored, has lately become more popular than cowboy boots among mathematical physicists. What are its properties? To be consistent with the properties of signed area A, the wedge product must be anticommutative and bilinear, and it must vanish when its factors are parallel:

WP1. v ^ w = -(w ^ v)
WP2. u ^ (v + w) = u ^ v + u ^ w
WP3. s(v ^ w) = (sv) ^ w = v ^ (sw) for any real number s
WP4. v ^ v = 0
WP5. (u ^ v) ^ w = u ^ (v ^ w)

Notice that these properties are very similar to those of the cross product XP1-5, except that the wedge product is associative (WP5) while the cross product was not. (Looking at WP5, it may occur to you that if v ^ w is a bivector, then u ^ v ^ w must be a trivector i.e. an oriented chunk of 3-D space. This is true, but it's the next rung of a ladder we don't want to climb right now). The reason for the similarity, and for the better behaviour of the wedge product, is that the wedge is a truly fundamental vector operation, whereas the cross product is sort of a 3-D wedge product in disguise. More on that later.

There will be pictures of bivectors in Section 5.4 to help your intuition, but for now we can learn something more about the wedge product simply by following the formal rules WP1-5. If we know what e_i ^ e_j are for all i and j, we know v ^ w for all v and w. For example, if v = v₁e₁ + v₂e₂ + v₃e₃ and w = w₁e₁ + w₂e₂ + w₃e₃ then

v ^ w = v₁w₁(e₁ ^ e₁) + v₁w₂(e₁ ^ e₂) + v₁w₃(e₁ ^ e₃)
+ v₂w₁(e₂ ^ e₁) + v₂w₂(e₂ ^ e₂) + v₂w₃(e₂ ^ e₃)
+ v₃w₁(e₃ ^ e₁) + v₃w₂(e₃ ^ e₂) + v₃w₃(e₃ ^ e₃). (5.5)

If we simplify this formula using the facts that the wedge product of a vector with itself is 0 and that changing the order of inputs changes the sign of the output, we obtain

v ^ w = (v₂w₃ - v₃w₂)(e₂ ^ e₃)
+ (v₃w₁ - v₁w₃)(e₃ ^ e₁)
+ (v₁w₂ - v₂w₁)(e₁ ^ e₂). (5.6)

In general, any bivector B in a 3-D space V has the form

B₁(e₂ ^ e₃) + B₂(e₃ ^ e₁) + B₃(e₁ ^ e₂). (5.7)

Notice that if you got really drunk, and somehow mistook e₂ ^ e₃ for e₁, e₃ ^ e₁ for e₂, and e₁ ^ e₂ for e₃, you might get the idea that B is a vector with three components (B₁, B₂, B₃). Something like this did happen in mathematical history, with the result that the wedge product of vectors in 3-D space was mistaken for a vector and named the "cross product" (notice the correspondence between Formulas (2.11) and (5.6)) even though the peculiar behaviour of cross product "vectors" with respect to mirrors was well known. This is also the reason that the angular velocity bivector is usually called a vector. Both cross products and angular velocity vectors are clearly defined, and you can use them without shame in cases where a vector is easier to picture than a bivector (that is, most of the time), but they do have some strange properties, such as nonassociativity and flipped reflections, that are ultimately due to the fact that they are bivectors masquerading as vectors.

5.4 Picturing Bivectors

In the last section we learned the rules for computing bivectors. Now we try to develop some intuition for what we have computed. Thus Figure 5.3 presents several pictures of the bivector e₁ ^ e₂, where e₁ and e₂ are orthogonal unit vectors lying in the plane of the paper.

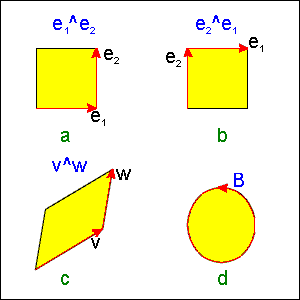
In Figure 5.3a we see the two vectors e₁ and e₂ head to tail, with the parallelogram they define shaded in. This shaded area, together with the arrows representing the vectors, is a picture of the bivector e₁ ^ e₂. A bivector, like a vector, does not have a location, and so the same drawing anywhere on the sheet represents the same bivector. If we draw the vectors with the tail of e₁ touching the head of e₂, as in Figure 5.3b, we have a picture of the bivector e₂ ^ e₁. This figure provides a clue to the geometric meaning of the sign difference between e₁ ^ e₂ and e₂ ^ e₁. It has to do with the direction taken in going round the shaded area: if you walk first along e₁ and then along e₂, as in the picture of e₁ ^ e₂, you are circling counterclockwise; if you walk first along e₂ and then along e₁, you are circling clockwise. Thus, just as a vector differs from a line segment in having a positive or negative direction, a bivector differs from a parallelogram in having a "circling direction" or orientation.

But a bivector differs from a parallelogram in another way as well: a bivector has no shape, and so any patch with the same area and orientation in the same plane is a picture of the same bivector. Thus the bivector v ^ w in Figure 5.3c is the same as e₁ ^ e₂, and so is the bivector B in Figure 5.3d.

Finally, Figure 5.4 shows that bivectors go through mirrors in an entirely intuitive way that explains the "flipped" reflections of cross products and angular velocities that alarmed us at the beginning of the chapter. For example, when e₁ and e₂ go through the mirror (which is seen edge-on in Figure 5.3e) the "circling direction" around the bivector changes from counterclockwise to clockwise, i.e. the wedge product is multiplied by -1, changing from e₁ ^ e₂ to -e₁ ^ e₂. It is only when we mistake e₁ ^ e₂ for e₃ and -e₁ ^ e₂ for -e₃ that we seem to have a vertical vector flipping upside-down when reflected in a vertical mirror.